Help Plotting Circles in Cartopy

[sheeny]

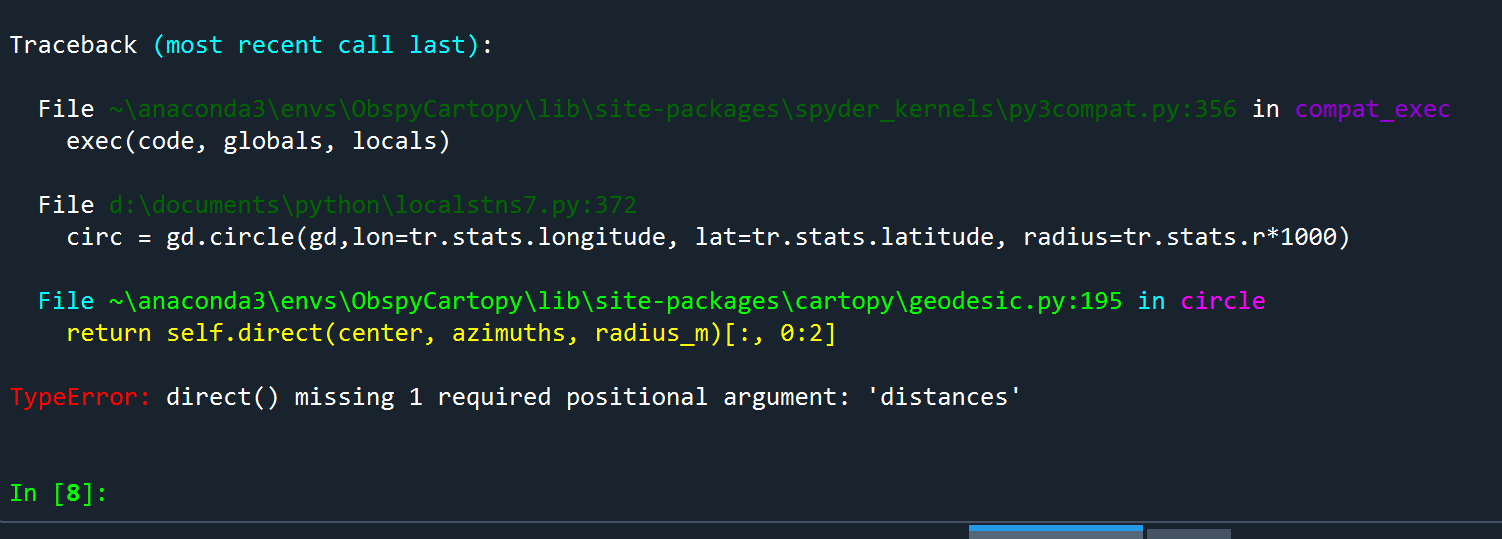
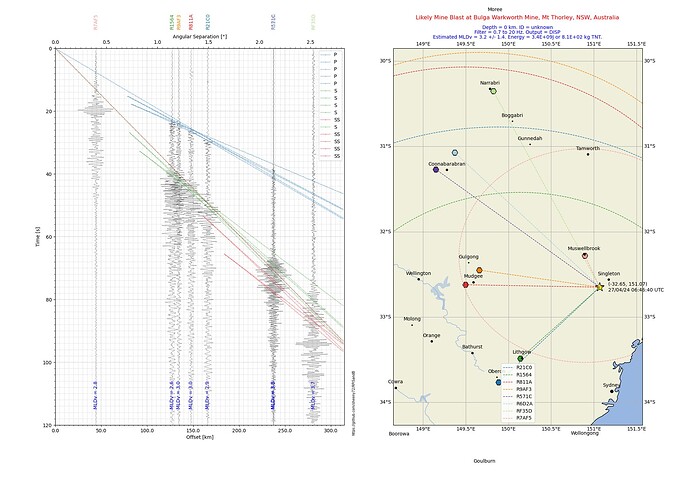
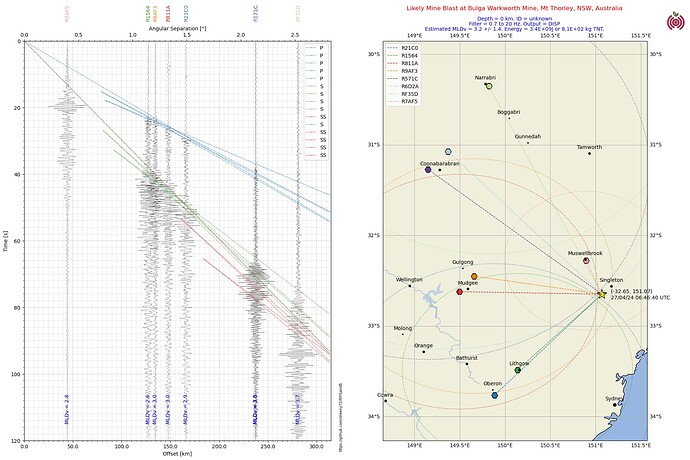
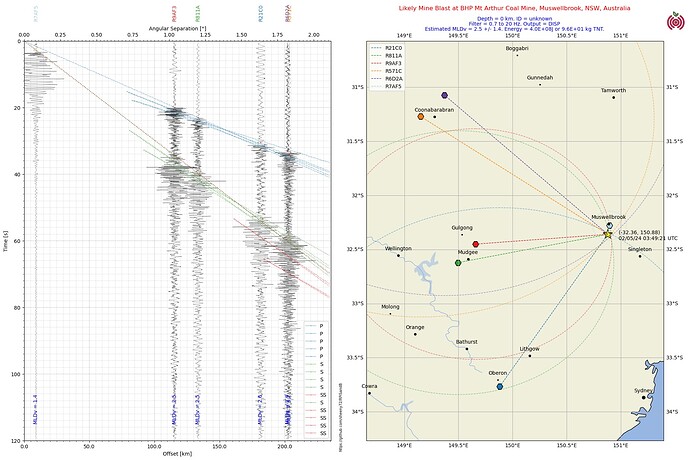
I am working on developing my LocalStns.py code to include a series of circles concentric around each station with a radius calculated from the difference in arrival times of the P and S phases. I am having trouble with either calculating the circle or plotting the circle.

Here is the error message I get:

I can’t see where the positional argument ‘distances’ is missing from.

Here is the full code:

# -*- coding: utf-8 -*-
"""
Created on Sun May 21 12:22:53 2023

@author: al72
"""

from obspy.clients.fdsn import Client
from obspy.core import UTCDateTime, Stream
import matplotlib.pyplot as plt
from obspy.taup import TauPyModel
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import numpy as np
import math
from matplotlib.transforms import blended_transform_factory
from matplotlib.cm import get_cmap
from obspy.geodetics import gps2dist_azimuth, kilometers2degrees, degrees2kilometers
import matplotlib.ticker as ticker
from cartopy.geodesic import Geodesic
import shapely.geometry as sgeom
gd = Geodesic

rs = Client('https://data.raspberryshake.org/')

# Build a station list of local stations so unwanted stations can be commented out
# as required to save typing
def stationList(sl):
    sl += ['R21C0']    #Oberon
    sl += ['R1564']    #Lithgow
    sl += ['R811A']    #Mudgee
    sl += ['R9AF3']    #Gulgong
    sl += ['R571C']    #Coonabarabran
    sl += ['R6D2A']    #Coonabarabran
    sl += ['RF35D']    #Narrabri
    sl += ['R7AF5']    #Muswellbrook
    #sl += ['R26B1']    #Murrumbateman
    #sl += ['R3756']    #Chatswood
    #sl += ['R9475']    #Sydney
    #sl += ['R6707']    #Gungahlin
    #sl += ['R69A2']    #Penrith
    #sl += ['RB18D']    #Canberra
    #sl += ['R9A9D']    #Brisbane
    #sl += ['RCF6A']    #Brisbane
    #sl += ['S6197']    #Heyfield
    #sl += ['RD371']    #Melbourne
    #sl += ['RC98F']    #Creswick
    #sl += ['RA20F']    #Broken Hill
    #sl += ['RC74C']    #Broken Hill
    #sl += ['RECF1']    #Koroit
    #sl += ['R4E78']    #Stawell
    #sl += ['RDD97']    #Melbourne
    #sl += ['R9CDF']    #Dandenong
    #sl += ['RBA56']    #Launceston
    #sl += ['RAA90']    #Scamander
    #sl += ['RA13F']    #Hobart
    #sl += ['R7A67']    #Hobart
    #sl += ['R0FFA']    #Hobart
    #sl += ['R54E6']    #Blanchetown
    #print(sl)
    return sl

# Build a list of ranges S-P times from S-P plots
pstimes = [20,
          15,
          18,
          18,
          28,
          29,
          25,
          11,
          ]

# Trace plotting routine for determining S - P time
def trplot (tr, j):
    fig1 = plt.figure(figsize=(10,7), dpi=100)       # set to page size in inches
    axtr = fig1.add_subplot(1,1,1)
    st1 = []
    st1 += tr
    axtr.plot(st1[0].times(reftime=eventTime), st1[0].data, lw=1, color='k')      # displacement waveform
    axtr.xaxis.set_major_locator(ticker.MultipleLocator(10))
    axtr.xaxis.set_minor_locator(ticker.AutoMinorLocator(10))
    axtr.grid(color='dimgray', ls = '-.', lw = 0.33)
    axtr.grid(color='dimgray', which='minor', ls = ':', lw = 0.33)
    fig1.suptitle(str(j), weight='black', color='b', size='large')      #Title of the figure
    plt.show()
    
# Build a stream of traces from each of the selected stations    
def buildStream(strm, op, rp):
    n = len(slist)      # n is the number of traces (stations) in the stream
    tr1 = []
    for i in range(0, n):
        inv = rs.get_stations(network='AM', station=slist[i], level='RESP')  # get the instrument response
        
        #read each epoch to find the one that's active for the event
        k=0
        while True:
            sta = inv[0][k]         #station metadata
            if sta.is_active(time=eventTime):
                break
            k += 1
        latS = sta.latitude     #active station latitude
        lonS = sta.longitude     #active station longitude
        #eleS = sta.elevation     #active station elevation is not required for this program
        print(sta)      # print the station on the console so you know which, if any, station fails to have data
        #find max and min lat and longs for map extents
        trace = rs.get_waveforms('AM', station=slist[i], location = "00", channel = '*HZ', starttime = start, endtime = end) #vertical geophone could be EHZ or SHZ
        trace.merge(method=0, fill_value='latest')         #fill in any gaps in the data to prevent a crash
        trace.detrend(type='demean')                       #detrend the data
        tr1 = trace.remove_response(inventory=inv,zero_mean=True,pre_filt=ft,output=op,water_level=60, plot=False) # convert to displacement so ML can be estimated
        # save data in the trace.stats for use later
        tr1[0].stats.distance = gps2dist_azimuth(latS, lonS, latE, lonE)[0] # distance from the event to the station in metres
        tr1[0].stats.latitude = latS        # save the station latitude from the inventory with the trace
        tr1[0].stats.longitude = lonS       # save the station longitude from the inventory with the trace
        tr1[0].stats.colour = colours[i % len(colours)]    # assign a colour to the station/trace
        tr1[0].stats.amp = np.abs(tr1[0].max()/1e-6)   # max amplitude in µm, µm/s or µm/s²
        if op == 'VEL':
            tr1[0].stats.mL = np.log10(tr1[0].stats.amp) + 2.6235*np.log10(tr1[0].stats.distance/1000) - 3.415   #ML by modified Tsuboi Empirical Formula
        elif op == 'ACC':
            tr1[0].stats.mL = np.log10(tr1[0].stats.amp) + 3.146*np.log10(tr1[0].stats.distance/1000) - 6.154
        else:
            tr1[0].stats.mL = np.log10(tr1[0].stats.amp) + 2.234*np.log10(tr1[0].stats.distance/1000) - 1.199
        strm += tr1
        if rp:
            trplot(tr1, i)
    #strm.plot(method='full', equal_scale=False)
    return strm #, nlat, xlat, nlon, xlon

# function to convert kilometres to degrees
def k2d(x):
    return kilometers2degrees(x)

# function to convert degrees to kilometres
def d2k(x):
    return degrees2kilometers(x)

# function to estimate distance in km from S - P arrival times
def distSP(t):
    range = 8e-7*math.pow(t,4)-3e-4*math.pow(t,3)+0.449*math.pow(t,2)+7.726*t
    return range

# Build a list of local places for the map
# Lat Long Data from https://www.latlong.net/
# format ['Name', latitude, longitude, markersize]
#comment out those not used to minimise typing
places = [['Oberon', -33.704922, 149.862900, 2],
          ['Bathurst', -33.419281, 149.577499, 4],
          ['Lithgow', -33.480930, 150.157410, 4],
          ['Mudgee', -32.590439, 149.588684, 4],
          ['Orange', -33.283333, 149.100006, 4],
          ['Molong', -33.092239, 148.870804, 2],
          ['Sydney', -33.868820, 151.209290, 6],
          ['Newcastle', -32.926670, 151.780014, 5],
          ['Wollongong', -34.427811, 150.893066, 5],
          ['Coonabarabran', -31.273911, 149.277420, 4],
          ['Gulgong', -32.362492, 149.532104, 2],
          ['Narrabri', -30.325060, 149.782974, 4],
          ['Moree', -29.463551, 149.841721, 4],
          ['Muswellbrook', -32.265221, 150.888184, 4],
          ['Singleton', -32.561111, 151.174591, 4],
          ['Tamworth', -31.092749, 150.932037, 4],
          ['Gunnedah', -30.976900, 150.251816, 2],
          ['Boggabri', -30.704121, 150.044098, 2],
          ['Boorowa', -34.437340, 148.717972, 2],
          ['Cowra', -33.828144, 148.677856, 4],
          ['Dubbo', -32.246380, 148.591263, 4],
          ['Wellington', -32.555988, 148.944824, 4],
          ['Goulburn', -34.754539, 149.717819, 4],
          ['Cooma', -36.235291, 149.125275, 4],
          ['Grafton', -29.690960, 152.932968, 4],
          ['Coffs Harbour', -30.296350, 153.115692, 4],
          ['Armidale', -30.512960, 151.669418, 4],
          ['Brisbane', -27.469770, 153.025131, 6],
          ['Canberra', -35.280937, 149.130005, 6],
          ['Albury', -36.073730, 146.913544, 4],
          ['Wagga Wagga', -35.114750, 147.369614, 4],
          ['Broken Hill', -31.955891, 141.465347, 4],
          ['Wilcannia', -31.558981, 143.378464, 4],
          ['Cobar', -31.494930, 145.840164, 4],
          ['Brewarrina', -29.960070, 146.855652, 2],
          ['Melbourne', -37.813629, 144.963058, 6],
          ['Bairnesdale', -37.825270, 147.628790, 4],
          ['Ballarat', -37.562160, 143.850250, 4],
          ['Hobart', -42.882137, 147.327194, 6],
          ['Launceston', -41.433224, 147.144089, 4]
          ]

# Enter event data (estimate by trial and error for unregistered events)    
eventTime = UTCDateTime(2024, 4, 27, 6, 46, 40) # (YYYY, m, d, H, M, S) **** Enter data****
latE = -32.65                                    # quake latitude + N -S **** Enter data****
lonE = 151.07                                    # quake longitude + E - W **** Enter data****
depth = 0                             # quake depth, km **** Enter data****
mag = 3.2                             # quake magnitude **** Enter data****
eventID = 'unknown'               # ID for the event **** Enter data****
locE = "Bulga Warkworth Mine, Mt Thorley, NSW, Australia"      # location name **** Enter data****

# perform range estimate plots
rplots = False
plotrs = True

# Make a list of stations
slist = []
stationList(slist)
# bandpass filter - select to suit system noise and range of quake
#ft = [0.09, 0.1, 0.8, 0.9]
#ft = [0.29, 0.3, 0.8, 0.9]
#ft = [0.49, 0.5, 2, 2.1]
#ft = [0.6, 0.7, 2, 2.1]       #distant quake
#ft = [0.6, 0.7, 3, 3.1]
#ft = [0.6, 0.7, 4, 4.1]
#ft = [0.6, 0.7, 6, 6.1]
#ft = [0.6, 0.7, 8, 8.1]
#ft = [0.9, 1, 10, 10.1]
#ft = [0.69, 0.7, 10, 10.1]
ft = [0.69, 0.7, 20, 20.1]
#ft = [2.9, 3, 20, 20.1]        #use for local quakes

if plotrs and (len(slist)!=len(pstimes)):
    print('Station and PS Times mismatch error!')

# Pretty paired colors. Reorder to have saturated colors first and remove
# some colors at the end. This cmap is compatible with obspy taup - credit to Mark Vanstone for this code.
cmap = get_cmap('Paired', lut=12)
colours = ['#%02x%02x%02x' % tuple(int(col * 255) for col in cmap(i)[:3]) for i in range(12)]
colours = colours[1:][::2][:-1] + colours[::2][:-1]
print(colours)
#colours = ['r', 'b', 'g', 'k', 'c', 'm', 'purple', 'orange', 'gold', 'midnightblue']    # array of colours for stations and phases
plist = ('P', 'S', 'SS')      # phase list for plotting

#set up the plot
delay = 0           # for future development for longer distance quakes - leave as 0 for now!
duration = 120       #adjust duration to get detail required
start = eventTime + delay   # for future development for longer distance quakes
end = start + duration      # for future development for longer distance quakes
output = 'DISP'
#output = 'VEL'
#output = 'ACC'
if output == 'VEL':
    mlabel = "MLVv"
    mLerr = 1.56
elif output =='ACC':
    mlabel = 'MLAv'
    mLerr = 1.89
else:
    mlabel = 'MLDv'
    mLerr = 1.40

# Build the stream of traces/stations
st = Stream()
buildStream(st, output, rplots)

#initialise map extents
minlat = latE
maxlat = latE
minlon = lonE
maxlon = lonE
n = len(st)
for i in range (0, n):  # build up map extents from station lat longs
        if st[i].stats.latitude < minlat:
            minlat = st[i].stats.latitude
        if st[i].stats.latitude > maxlat:
            maxlat = st[i].stats.latitude
        if st[i].stats.longitude < minlon:
            minlon = st[i].stats.longitude
        if st[i].stats.longitude > maxlon:
            maxlon = st[i].stats.longitude
        if plotrs:
            #add range to trace stats
            st[i].stats.r = distSP(pstimes[i])
            #print(st[i].stats.r)

#set up the figure
fig = plt.figure(figsize=(20,14), dpi=100)       # set to page size in inches

#build the section plot
ax1 = fig.add_subplot(1,2,1)
st.plot(type='section', plot_dx=50e3, recordlength=duration, time_down=True, linewidth=.3, alpha=0.8, grid_linewidth=.25, show=False, fig=fig)
ax1.xaxis.set_minor_locator(ticker.AutoMinorLocator(10))
ax1.yaxis.set_minor_locator(ticker.AutoMinorLocator(10))

# Plot customization: Add station labels to offset axis
ax = ax1.axes
transform = blended_transform_factory(ax.transData, ax.transAxes)
axt, axb = ax1.get_ylim()   #get the top and bottom limits of the axes
#print(axt, axb)
j=0
mLav = 0
for t in st:
    ax.text(t.stats.distance / 1e3, 1.05, t.stats.station, rotation=90,
            va="bottom", ha="center", color=t.stats.colour, transform=transform, zorder=10)
    ax.text(t.stats.distance / 1e3, axt-5, mlabel+' = '+str(np.round(t.stats.mL,1)), rotation=90,
            va="bottom", ha="center", color = 'b', zorder=10)    #print ML estimates
    mLav += t.stats.mL  
    j += 1

#calculate average ML estimate
mLav = mLav/j

#Calculate Earthquake Total Energy
qenergy = 10**(1.5*mLav+4.8)

#setup secondary x axis
secax_x1 = ax1.secondary_xaxis('top', functions = (k2d, d2k))   #secondary axis in degrees separation
secax_x1.set_xlabel('Angular Separation [°]')
secax_x1.xaxis.set_minor_locator(ticker.AutoMinorLocator(10))

#plot arrivals times
model = TauPyModel(model="iasp91")

axl, axr = ax1.get_xlim()   # get the left and right limits of the section plot
if axl<0:           #if axl is negative, make it zero to start the range for phase plots
    axl=0
#axl = 90      # uncomment to adjust left side of section plot, kms
ax1.set_xlim(left = axl)
for j in range (int(axl), int(axr)):    # plot phase arrivals every kilometre
    arr = model.get_travel_times(depth, k2d(j), phase_list=plist)
    n = len(arr)
    for i in range(0,n):
        if j == int(axr)-1:
            ax.plot(j, arr[i].time, marker='o', markersize=1, color = colours[plist.index(arr[i].name) % len(colours)], alpha=0.3, label = arr[i].name)
        else:
            ax.plot(j, arr[i].time, marker='o', markersize=1, color = colours[plist.index(arr[i].name) % len(colours)], alpha=0.3)
#        if j/50 == int(j/50):       # periodically plot the phase name
#            ax.text(j, arr[i].time, arr[i].name, color=colours[plist.index(arr[i].name) % len(colours)], alpha=0.5, ha='center', va='center')
    j+=1
ax.grid(color='dimgray', ls = '-.', lw = 0.33)
ax.grid(color='dimgray', which='minor', ls = ':', lw = 0.33)
ax.legend(loc = 'best')
                
#plot the map
ax2 = fig.add_subplot(1,2,2, projection=ccrs.PlateCarree())
mt = maxlat+0.5    # latitude of top of map
mb = minlat-0.5    # latitude of the bottom of the map
ml = minlon-0.5    # longitude of the left side of the map
mr = maxlon+0.5    # longitude of the right side of the map
ax2.set_extent([ml,mr,mt,mb], crs=ccrs.PlateCarree())
#ax2.coastlines(resolution='110m')  # use for large scale maps
#ax2.stock_img()                    # use for large scale maps

# Create a features
states_provinces = cfeature.NaturalEarthFeature(
    category='cultural',
    name='admin_1_states_provinces_lines',
    scale='50m',
    facecolor='none')
ax2.add_feature(cfeature.LAND)
ax2.add_feature(cfeature.OCEAN)
ax2.add_feature(cfeature.COASTLINE)
ax2.add_feature(states_provinces, edgecolor='gray')
ax2.add_feature(cfeature.LAKES, alpha=0.5)
ax2.add_feature(cfeature.RIVERS)
ax2.gridlines(draw_labels=True)
#plot event/earthquake position on map
ax2.plot(lonE, latE,
     color='yellow', marker='*', markersize=20, markeredgecolor='black',
     transform=ccrs.Geodetic(),
     )
# print the lat, long, and event time beside the event marker
ax2.text(lonE+0.1, latE-0.05, "("+str(latE)+", "+str(lonE)+")\n"+eventTime.strftime('%d/%m/%y %H:%M:%S UTC'), ha='left')

#plot station positions on map
for tr in st:
    ax2.plot(tr.stats.longitude, tr.stats.latitude,
             color=tr.stats.colour, marker='H', markersize=12, markeredgecolor='black',
             transform=ccrs.Geodetic(),
             )
    ax2.plot([tr.stats.longitude, lonE], [tr.stats.latitude, latE],
         color=tr.stats.colour, linewidth=1, linestyle='--', 
         transform=ccrs.Geodetic(), label = tr.stats.station,
         )
    if plotrs:
        circ = gd.circle(gd,lon=tr.stats.longitude, lat=tr.stats.latitude, radius=tr.stats.r*1000)
        ax2.plot(sgeom.Polygon(circ),
                 color=tr.stats.colour, linewidth=1, linestyle='--',
                 transform=ccrs.Geodetic()
                 )
ax2.legend()

#plot only the places inside the map boundary
for pl in places:
    if pl[2]>ml and pl[2]<mr:   #test for longtiude inside the map
        if pl[1]mb:   #test for latitude inside the map
            ax2.plot(pl[2], pl[1], color='k', marker='o', markersize=pl[3], markeredgecolor='k', transform=ccrs.Geodetic(), label=pl[0])
            ax2.text(pl[2], pl[1]+0.05, pl[0], horizontalalignment='center', transform=ccrs.Geodetic())

#add Notes
#fig.text(0.75, 0.96, 'M'+str(mag)+' Earthquake at '+locE, ha='center', size = 'large', color='r')  # use for identified earthquakes
fig.text(0.75, 0.96, 'Likely Mine Blast at '+locE, ha='center', size = 'large', color='r')     # use for unidentified events
fig.text(0.75, 0.94, 'Depth = '+str(depth)+' km. ID = '+eventID, ha='center', color = 'b')
fig.text(0.75, 0.93, 'Filter = '+str(ft[1])+' to '+str(ft[2])+' Hz. Output = '+output, ha='center', color = 'b')
fig.text(0.75, 0.92, 'Estimated '+mlabel+' = '+str(np.round(mLav,1))+' +/- '+str(mLerr)+'. Energy = '+f"{qenergy:0.1E}"+'J or '+f"{qenergy/4.18e6:0.1E}"+' kg TNT.', ha='center', color = 'b')

# add github repository address for code
fig.text(0.51, 0.1,'https://github.com/sheeny72/RPiSandB', size='x-small', rotation=90)

# plot logos
rsl = plt.imread("RS logo.png")
newaxr = fig.add_axes([0.935, 0.915, 0.05, 0.05], anchor='NE', zorder=-1)
newaxr.imshow(rsl)
newaxr.axis('off')

plt.subplots_adjust(wspace=0.1)

# add a plt.savefig(filename) line here if required.

plt.show()

FYI the code is intended to be run twice:

The first time with rplots = True in line 198, and plotrs = False in line 199. This produces a series of high resolution trace plots to determine the S - P arrival times for each station which are then manually entered into the array pstimes (in lines 64 to 72).

Once the pstimes array is complete, the code is run again with rplots = False in line 198 and plotrs = True in line 199. This is the state in which I have presented the code above.

The intent is to plot radius cicles around each station in the same was as EQ Locator does, hopefully to speed up the trial and error process of finding the quake or mine blast location, and to give some graphical indication of the precision of the final location estimate.

The code where the circle is calculated and plotted is in lines 371 to 376.

Thanks,

Al.

[Stormchaser]

This looks great sheeny!

The issue was in the lines following if plotrs (372). I’ve slightly modified them and commented on what the new lines do:

    if plotrs:
        # initiate Geodesic
        gd = Geodesic()
        # create the circle representing the range
        circ = gd.circle(lon=tr.stats.longitude, lat=tr.stats.latitude, radius=tr.stats.r*1000)
        # create a shapely polygon from the circle coordinates
        circ_polygon = sgeom.Polygon(circ)
        # extract the exterior coordinates of the polygon
        x, y = circ_polygon.exterior.xy
        # plot the exterior of the polygon
        ax2.plot(x, y, color=tr.stats.colour, linewidth=1, linestyle='--', transform=ccrs.Geodetic())

There were two problems. The first was that, in the original line, gd.circle was called as if it were a class method requiring the class itself as the first parameter, generating the error. This can be avoided by initializing Geodesic (gd) before that (without passing it as an argument) and then creating the circle. Geodesic is, as many things with Python are, very specific in how has to be set up.

Now that we have gd set up, we need to generate the circle polygon to be displayed on the map. The original plot function would not work because the basic Matplotlib plot is not supported in this way. You have to extract the polygon’s exterior coordinates first and then pass these to Matplotlib.

Now the code runs without errors, and I got the image above. Always nice work from you!

[sheeny]

G’Day Stormchaser,

Thanks so much for your help! That should get me over the problem I was stuck on!

Hmm looks like I have a problem to solve with the radius calculation though! lol!

thanks again!

Al.

[Stormchaser]

Good evening to you sheeny,

You’re very welcome! It was a bit tricky but wasn’t so convoluted in the end, which was good for both of us!

Yes, I noticed that the radiuses were a bit larger than what you (I assumed) intended, but I didn’t know if you did this on purpose to test something during the code development.

No problem!

[sheeny]

FWIW, the error in the radius calculations was a bit of sloppy transposing on my part (from Excel to Python) with errors in two coefficients.

The correct calculation is:

# function to estimate distance in km from S - P arrival times
def distSP(t):
    range = 8e-7*math.pow(t,4)-3e-4*math.pow(t,3)+0.0449*math.pow(t,2)+7.276*t
    return range

and the result looks like this:

Which only goes to show the difficulty in estimating the true arrival time of the P and S waves in weak signals. The trace from R7AF5 has a weak P arrival as it is arriving flat so there’s little to no vertical movement to detect on the EHZ sensor and the P arrival at RF35D is weak due to distance, so both these estimates are poor.

I’ll have to think about whether the extra work in using the S-P time estimates is worth it…

Al.

[Stormchaser]

Hello sheeny,

Honestly, this looks great to me! I think this is a great step in the right direction, as the circles clearly appear to converge where the event epicenter was located.

A suggestion that comes to mind is that you could plot an “uncertainty circle” (or ellipse) around the averaged center where the circles meet, which would provide your code best evaluation of the possible epicenter.

[sheeny]

G’Day Stormchaser,

I’ve had a play with it a couple of times since, and while the workflow is more involved I think it definitely helps to find the epicentre, and adds confidence to the epicentre position. Just more tools to work with. ;o)

Al.

[Stormchaser]

You can definitely never have too many tools, plots, excel spreadsheets, and code to work with! That’s a guarantee.

[sheeny]

True.

Two things I’ve noticed after playing with this:

1. The circles give a valuable indication of the precision of the measurements;
2. the way it’s implemented, the procedure can be iterative - by that I mean, some traces will have very clear P and S arrivals so confidence in these radii are good. Where one or both arrivals is not so clear, small corrections can be made to better agree with the intersections of those we are confident in. After all, it’s hard to get a good estimate if the arrival isn’t as clear as we’d like! These P and S times are plotted on the section plot as points to directly compare with the theoretical arrival times, so it’s a good feedback process for confidence in both timing and location. For example:

If you look really closely at the section plot you’ll see a red dot on each trace corresponding to the P arrival time, and a yellow dot corresponding to the S arrival time ( I changed from blue to yellow when the plot was densely black to make it more visible, but I think I’ll have to change to either red or green for cases like this where the trace isn’t so black).

Al.