This is from a Raspberry Shake that a colleague of mine is hosting in his garden (so I have a decent baseline with another Shake at my place). The tweet is in German (sorry) but you get the idea I guess. The four helicopters passed almost exactly over the station and the “groundshaking” noise coupled into the seismometer. My colleague explains how to compute the speed of the helicopters (ca 200km/h or 110kts) from the Doppler shift.
Enjoy
HBE
Not sure that I totally follow his calculation … but he does end up with about the right answer, so it obviously works for him.
There are a few problems with trying to estimate speed from these traces, the most important one is that (as in this case) the helicopter has to fly pretty much directly overhead. Assuming that to be the case, the calculation using the only really measurable parameters (approach/depart frequencies) is non trivial. At least if you want an accurate answer.
You can’t just take the mid-frequency and assume that is the “transmitted” frequency - although doing so for a quick calculation gives an approximately correct answer.
This is because the frequency shift on approach and departure is NOT equal.
Looking at the formula for doppler shift:
f = f₀(v + vr)/(v + vs)
f = Observed frequency
f₀ = Emitted frequency
v = Wave velocity (speed of sound)
vr = Receiver velocity
vs = Source velocity
Since we are standing still, this simplifies a bit to:
f = f₀(v)/(v + vs)
So everything is constant, except that vs goes from positive to negative.
In one case we are dividing f₀(v) by some number PLUS the speed, and in the other that same number MINUS the speed. The two numbers are different.
Anyway, we have some of the info for the two cases, so we have two equations, one for the approach and one for the departure:
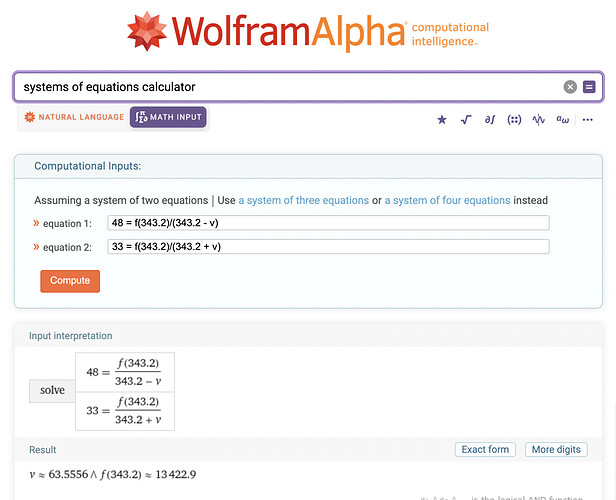
48 = f(343.2)/(343.2 - vs)
33 = f(343.2)/(343.2 + vs)
Hmm… simultaneous equations … always hated them 
Also, not really quite enough info to solve easily.
But fortunately WolframAlpha has a solver we can use:
It solves itteratively, so the numbers are approximate, but good enough.
The velocity of the helicopter is 63.5556m/s which is 228 km/h, and the emitted frequency is 13.433/343.2 = 39.14 Hz
Right. And that is actually just a linear system of 2 equations in two variabes, you can rewrite it to (Vs=speed of sound):
48 HzVs -48Hzv - fVs = 0
and
33HzVs +33HzVs -fVs =0
Subtract the two equations to eliminate f , and then solve for v . No need for a numerical solution.
HB
Yes, it simplifies significantly if you don’t want the “transmitted” frequency.
I should have thought about that, because even if I did want it, it is easier to do it the way you suggest, then go back and plug the values in to get that.
