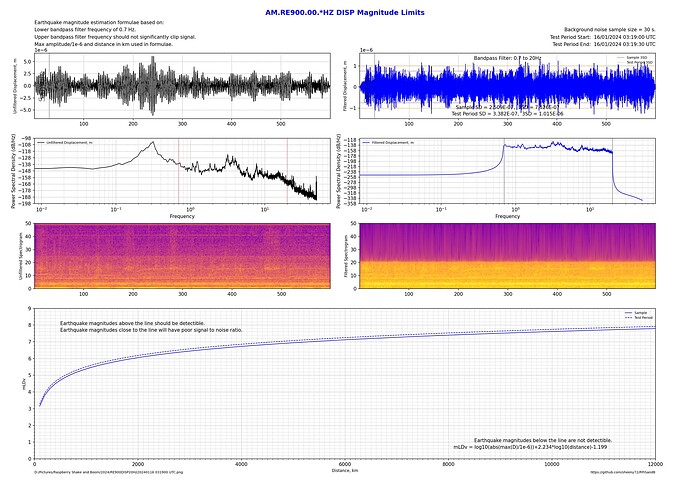
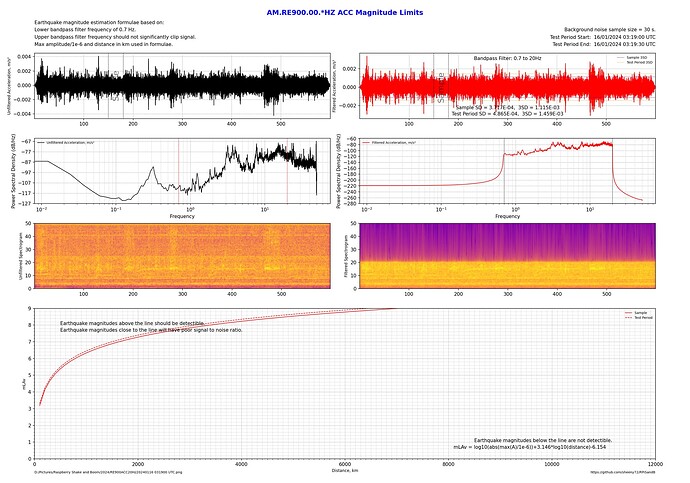
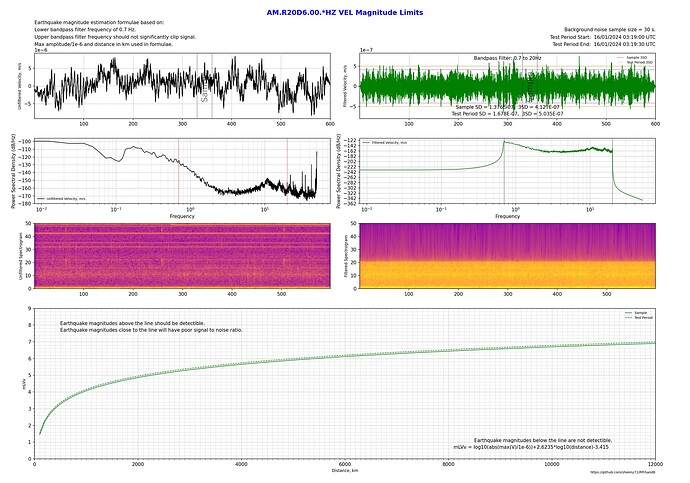
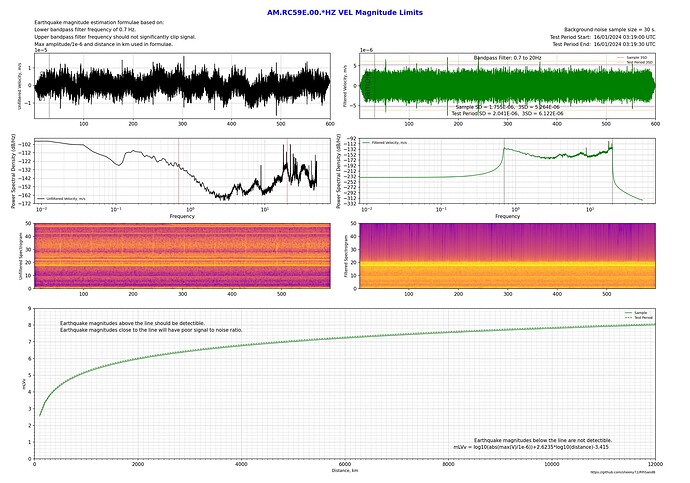
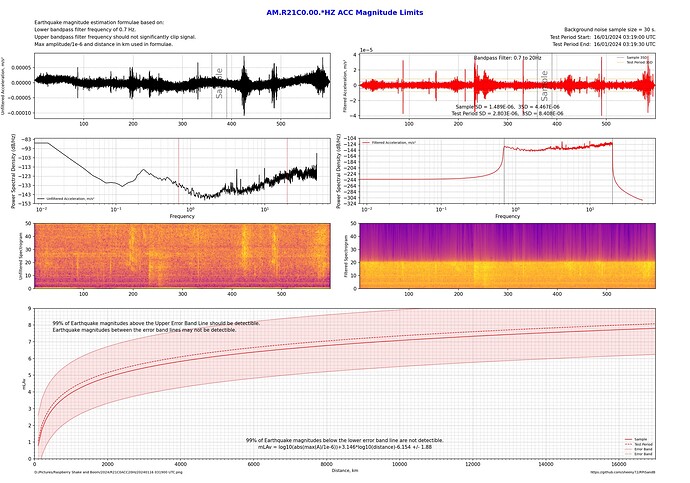
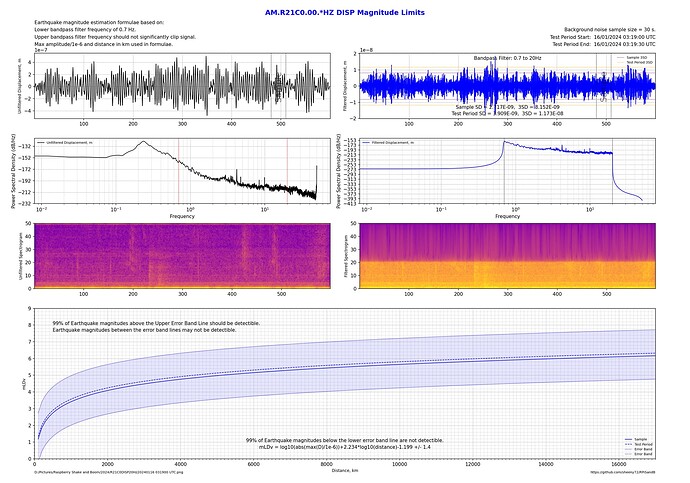
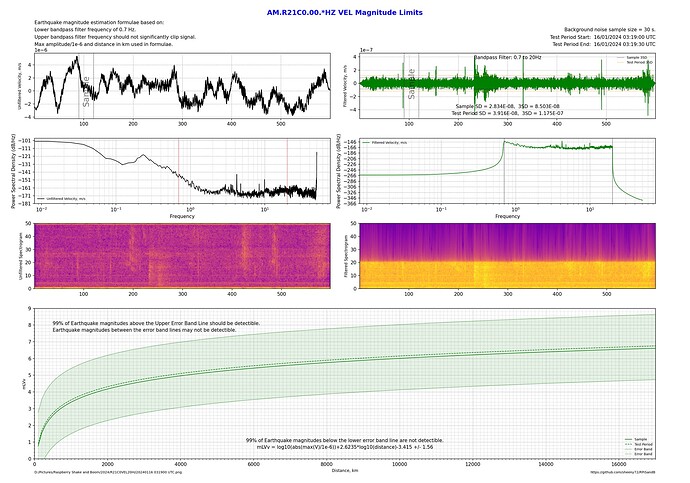
After playing around with multiple shakes doing section plots while chasing small local unregistered earthquakes and mine blasts, I found a lot of variation in what some stations can detect. For example, I might get a good signal on a station when using displacement for the output, but it’s unreadable in velocity and acceleration plots. Other times it might be acceleration that’s good but velocity and displacement aren’t.
This doesn’t just depend on the level of background noise, but also on the frequencies present in the noise and the choice of filter frequencies used.
I’ve written a python program to quantitatively measure background noise and determine what magnitude earthquakes should be detectable or not for a given station, filter frequencies and output.
Note: to compare the images, hover over the image and then click the dark bar at the bottom of the image. This will open the images so they can be readily clicked back and forth.
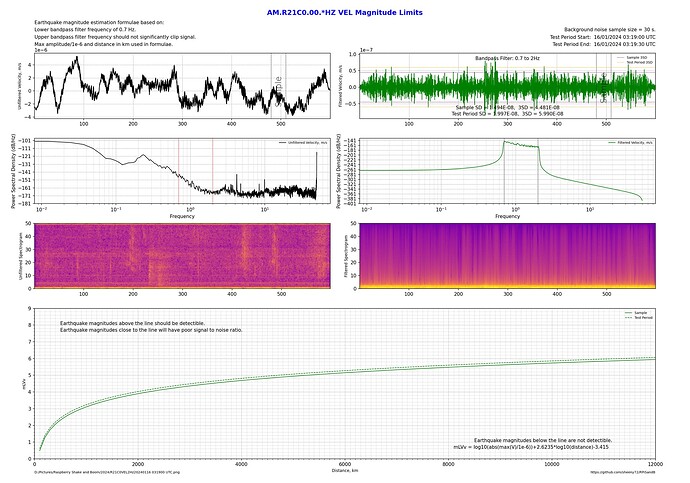
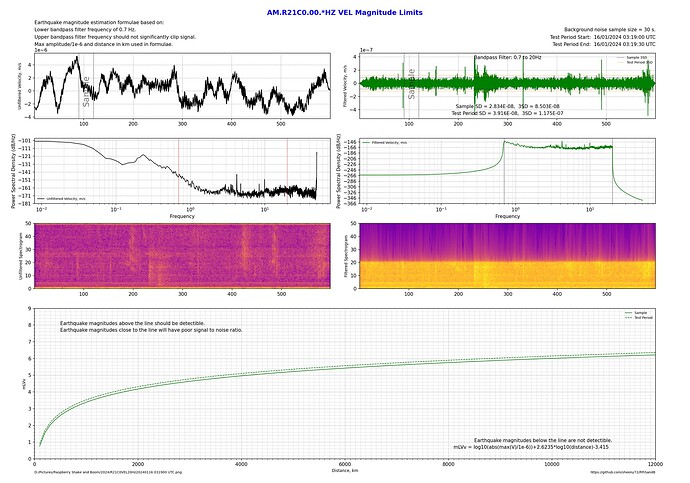
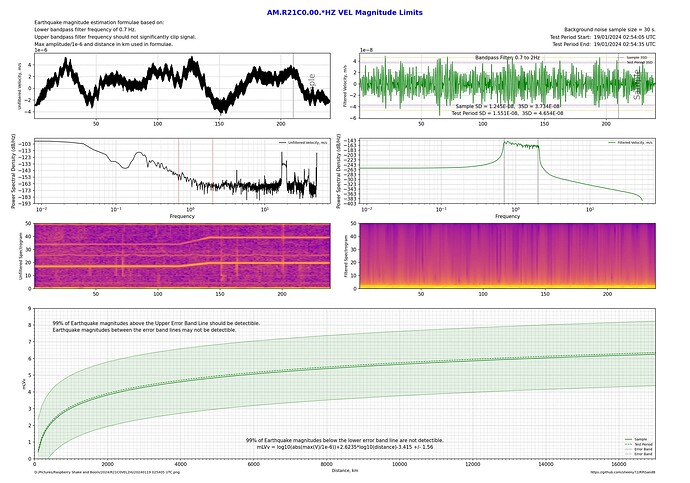
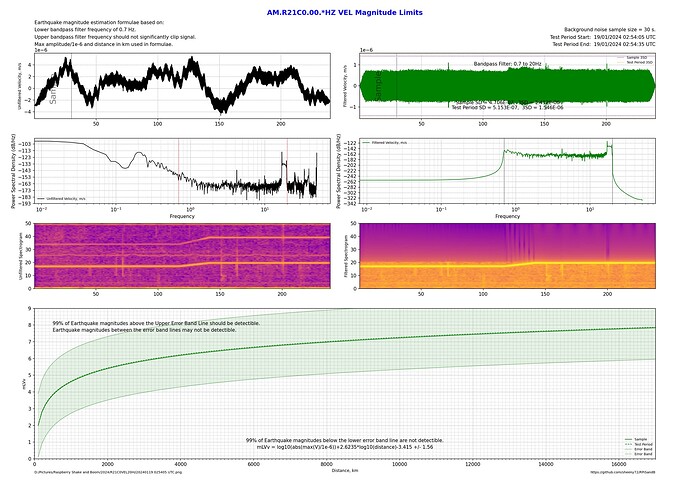
These two plots are on my station (R21C0), both at the same time, just the filter top frequency has changed. By flicking from one image to the other it can be seen that a 2Hz upper bandpass limit performs better by about 0.2 magnitudes over the whole range of distances.
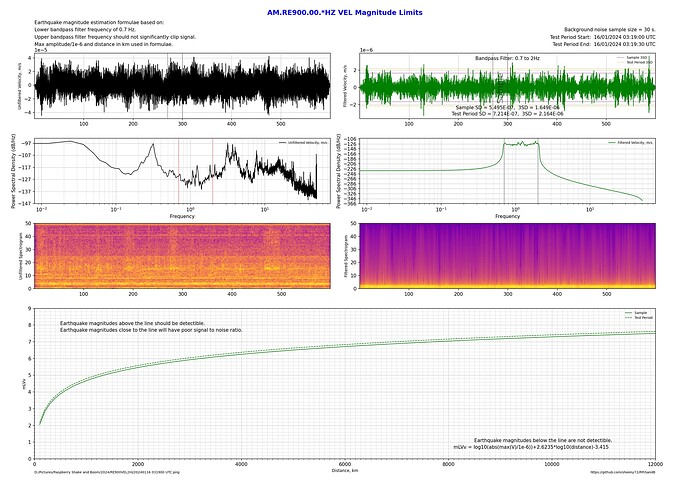
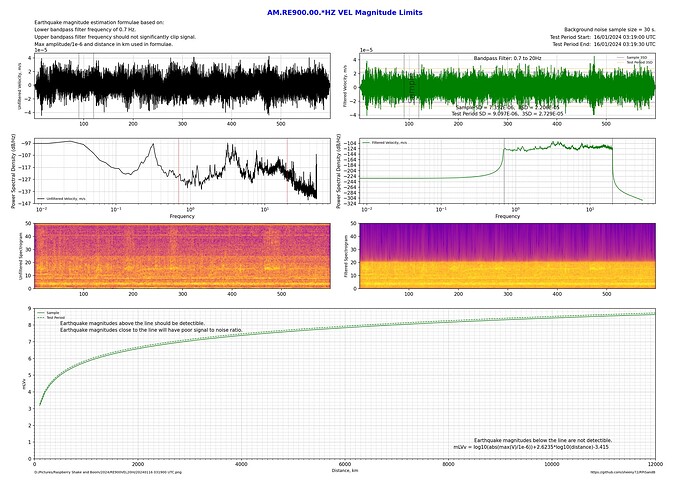
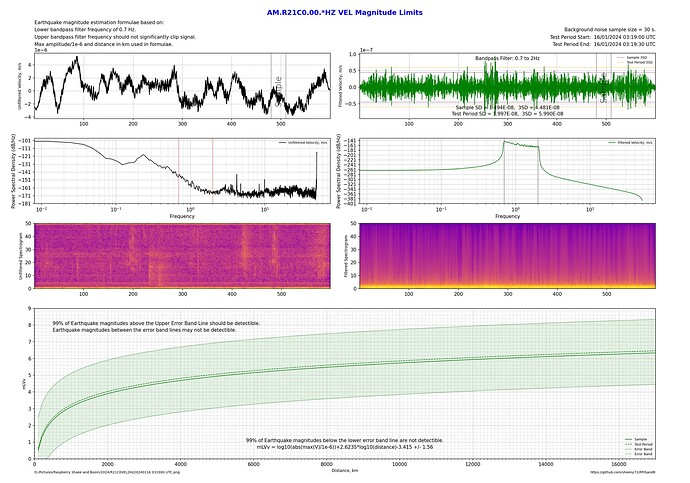
Compare this to a station installed right in the centre of Sydney:
By flicking back and forth between these 2 plots shows about a 1 magnitude difference between a 2Hz upper bandpass limit and the 20Hz upper bandpass limit!
Of course, it’s also possible to compare a relatively quiet country installation with one in the city with all the additional cultural noise.
Here’s the same station in Sydney comparing Displacement, Velocity and Acceleration outputs with a maximum bandpass frequency of 20 Hz as a sort of worst case scenario:
Clearly when there’s a lot of high frequency noise, apart from using a narrow bandpass filter such as 0.7 to 2 Hz, the use of Displacement also biases the lower frequencies so a better signal to noise ratio can be achieved.
This tool could also be used to quantify the effect of moving a Shake, or adding or modifying a vault, or the effect of a new noise source nearby, etc.
The code is available on Github: GitHub - sheeny72/RPiSandB: Python programs for Raspberry Shake and Boom seismometers and infrasound detectors.
I’ll share it here as well:
# -*- coding: utf-8 -*-
"""
Created on Tue Jan 16 14:56:51 2024
@author: al72
Raspberry Shake Magnitude Limits Estimator
Uses background noise measured on the Shake to estimate the minimum magnitude
earthquake detectible at any given distance.
Can be used to quantitatively compare one Shake installation and environment with another.
Can be used to compare differences in filter bands based on existing noise at the Shake.
Can be used to compare outputs (DISP v VEL v ACC) which are influenced by the
frequencies present in the background noise.
Based on magnitude estimation formulae empirically modified from the Tsuboi method
to suit 0.7 Hz lower band pass frequency for use on vertical geophone sensors on
Raspberry Shakes.
While this can be used on other sensors for comparative purposes, the accuracy of
any magnitude estimates is questionable.
"""
from obspy.clients.fdsn import Client
from obspy.core import UTCDateTime
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator
rs = Client('https://data.raspberryshake.org/')
def divTrace(tr, n): #divide trace into n equal parts for background noise determination
return tr.__div__(n)
def grid(ax): #pass axis
ax.grid(color='dimgray', ls = '-.', lw = 0.33)
ax.grid(color='dimgray', which='minor', ls = ':', lw = 0.33)
bnstart = UTCDateTime(2024, 1, 16, 3, 19, 0) # (YYYY, m, d, H, M, S) **** Enter data****
bnend = bnstart + 600
# set the station name and download the response information
stn = 'R21C0' # station name
nw = 'AM' # network name
ch = '*HZ' # ENx = accelerometer channels; EHx or SHZ = geophone channels... ONLY VALID FOR GEOPHONE CHANNELS!
#oput = 'DISP' # output - DISP = Displacement, VEL = Velocity, ACC = Acceleration
oput = 'VEL'
#oput = 'ACC'
inv = rs.get_stations(network=nw, station=stn, level='RESP') # get the instrument response
# bandpass filter - select to suit system noise and range of quake
filt = [0.69, 0.7, 2, 2.1] #distant quake
#filt = [0.69, 0.7, 3, 3.1]
#filt = [0.69, 0.7, 4, 4.1]
#filt = [0.69, 0.7, 6, 6.1]
#filt = [0.69, 0.7, 8, 8.1]
#filt = [0.69, 0.7, 10, 10.1]
filt = [0.69, 0.7, 20, 20.1]
#filt = [0.69, 0.7, 49, 50]
#get waveform for background noise and copy it for independent removal of instrument response
bn0 = rs.get_waveforms('AM', stn, '00', ch, bnstart, bnend)
bn0.merge(method=0, fill_value='latest') #fill in any gaps in the data to prevent a crash
bn0.detrend(type='demean') #demean the data
bn1 = bn0.copy() #copy for unfiltered trace
#Create background noise traces
bnfilt = bn0.remove_response(inventory=inv,pre_filt=filt,output=oput,water_level=60, plot=False) # filter the trace
bnraw = bn1.remove_response(inventory=inv,output=oput, plot=False) # unfiltered output
# Calculate background noise limits using standard deviation
bnxstd = bnfilt[0].std() # cakculate SD for whole test period
bnsamp = 30 #sample size in seconds
bns = int((bnend - bnstart)/bnsamp) #calculate the number of samples in the background noise trace
bnf = divTrace(bnfilt[0],bns) #divide the background noise trace into equal sample traces
for j in range (0, bns): #find the sample interval with the minimum background noise amplitude
if j == 0:
bnfstd = abs(bnf[j].std())
bnftime = bnf[j].stats.starttime
elif abs(bnf[j].std()) < bnfstd:
bnfstd = abs(bnf[j].std())
bnftime = bnf[j].stats.starttime
mv = []
mLv = []
dist = []
for d in range (0,120):
dist.append((d+1)*100)
if oput == 'DISP':
mLv.append(np.log10(abs(bnfstd*3/1e-6))+2.234*np.log10(dist[d])-1.199) #calculate estimate magnitude
mv.append(np.log10(abs(bnxstd*3/1e-6))+2.234*np.log10(dist[d])-1.199) #calculate estimate magnitude
elif oput == 'ACC':
mLv.append(np.log10(abs(bnfstd*3/1e-6))+3.146*np.log10(dist[d])-6.154) #calculate estimate magnitude
mv.append(np.log10(abs(bnxstd*3/1e-6))+3.146*np.log10(dist[d])-6.154) #calculate estimate magnitude
else:
mLv.append(np.log10(abs(bnfstd*3/1e-6))+2.6235*np.log10(dist[d])-3.415) #calculate estimate magnitude
mv.append(np.log10(abs(bnxstd*3/1e-6))+2.6235*np.log10(dist[d])-3.415) #calculate estimate magnitude
if oput == 'DISP':
colour = 'b'
ml = 'mLDv'
heading = 'Displacement, m'
eq = 'mLDv = log10(abs(max(D)/1e-6))+2.234*log10(distance)-1.199'
elif oput =='ACC':
colour = 'r'
ml = 'mLAv'
heading = 'Acceleration, m/s²'
eq = 'mLAv = log10(abs(max(A)/1e-6))+3.146*log10(distance)-6.154'
else:
colour = 'g'
ml = 'mLVv'
heading = 'Velocity, m/s'
eq = 'mLVv = log10(abs(max(V)/1e-6))+2.6235*log10(distance)-3.415'
fig = plt.figure(figsize=(20, 14), dpi=150) # set to page size in inches
ax1 = fig.add_subplot(5,2,1) # raw waveform
ax2 = fig.add_subplot(5,2,2) # filtered waveform
ax3 = fig.add_subplot(5,2,3) # raw PSD
ax4 = fig.add_subplot(5,2,4) # filtered PSD
ax5 = fig.add_subplot(5,2,5) # raw spectrogram
ax6 = fig.add_subplot(5,2,6) # spare / notes
ax7 = fig.add_subplot(5,2,(7,10)) # magnitude limit Graph
fig.suptitle(nw+'.'+stn+'.00.'+ch+' '+oput+' Magnitude Limits', weight='black', color='b', size='x-large') #Title of the figure
ax1.plot(bn1[0].times(reftime=bnstart), bn1[0].data, lw=1, color='k') # raw waveform
ax1.set_ylabel('Unfiltered '+heading, size='small')
ax1.margins(x=0)
ax1.axvline(x=bnftime-bnstart, linewidth=1, linestyle='dotted', color='k')
ax1.axvline(x=(bnftime-bnstart)+bnsamp, linewidth=1, linestyle='dotted', color='k')
ax1.text(bnftime-bnstart+bnsamp/2, 0, 'Sample', size = 'xx-large', alpha = 0.5, rotation = 90, ha = 'center', va = 'center')
grid(ax1)
ax2.plot(bn1[0].times(reftime=bnstart), bn0[0].data, lw=1, color=colour) # filtered waveform
ax2.set_ylabel('Filtered '+heading, size='small')
ax2.margins(x=0)
ax2b, ax2t = ax2.get_ylim()
ax2.text(300, ax2t*.8, 'Bandpass Filter: '+str(filt[1])+" to "+str(filt[2])+"Hz", ha = 'center')
ax2.text(300, ax2b*0.7, 'Sample SD = '+f"{bnfstd:.3E}"+', 3SD = '+f"{(3*bnfstd):.3E}", ha = 'center')
ax2.text(300, ax2b*0.9, 'Test Period SD = '+f"{bnxstd:.3E}"+', 3SD = '+f"{(3*bnxstd):.3E}", ha = 'center')
ax2.axvline(x=bnftime-bnstart, linewidth=1, linestyle='dotted', color='k')
ax2.axvline(x=(bnftime-bnstart)+bnsamp, linewidth=1, linestyle='dotted', color='k')
ax2.text(bnftime-bnstart+bnsamp/2, 0, 'Sample', size = 'xx-large', alpha = 0.5, rotation = 90, ha = 'center', va = 'center')
ax2.axhline(y=3*bnfstd, linewidth=1, linestyle='dotted', color='purple', label = 'Sample 3SD')
ax2.axhline(y=-3*bnfstd, linewidth=1, linestyle='dotted', color='purple')
ax2.axhline(y=3*bnxstd, linewidth=1, linestyle='dotted', color='orange', label = 'Test Period 3SD')
ax2.axhline(y=-3*bnxstd, linewidth=1, linestyle='dotted', color='orange')
grid(ax2)
ax2.legend(frameon=False, fontsize='x-small', loc = 'upper right')
#plot PSD
#calculate NFFT for PSD
nfft = 8192
ax3.psd(x=bn1[0], NFFT=nfft, noverlap=0, Fs=100, color='k', lw=1, label='Unfiltered '+heading) # velocity PSD raw data comment out if not required/desired
ax3.legend(frameon=False, fontsize='x-small')
ax3.set_xscale('log') #use logarithmic scale on PSD
ax3.axvline(x=filt[1], linewidth=1, linestyle='dotted', color='r')
ax3.axvline(x=filt[2], linewidth=1, linestyle='dotted', color='r')
grid(ax3)
ax4.psd(x=bn0[0], NFFT=nfft, noverlap=0, Fs=100, color=colour, lw=1, label='Filtered '+heading) # velocity PSD raw data comment out if not required/desired
ax4.legend(frameon=False, fontsize='x-small')
ax4.set_xscale('log') #use logarithmic scale on PSD
ax4.axvline(x=filt[1], linewidth=1, linestyle='dotted', color='k')
ax4.axvline(x=filt[2], linewidth=1, linestyle='dotted', color='k')
grid(ax4)
ax5.specgram(x=bn1[0], NFFT=256, noverlap=128, Fs=100, cmap='plasma') # raw spectrogram
ax5.set_ylabel("Unfiltered Spectrogram",size='small')
ax6.specgram(x=bn0[0], NFFT=256, noverlap=128, Fs=100, cmap='plasma') # raw spectrogram
ax6.set_ylabel("Filtered Spectrogram",size='small')
ax7.plot(dist, mLv, lw=1, color=colour, label = 'Sample')
ax7.plot(dist, mv, lw=1, color=colour, linestyle = '--', label = 'Test Period')
ax7.set_ylabel(ml,size='small')
ax7.set_xlabel("Distance, km",size='small')
ax7.margins(x=0)
ax7.margins(y=0)
ax7.set_ylim(0, 9)
ax7.set_xlim(0, 12000)
ax7.xaxis.set_minor_locator(AutoMinorLocator(20))
ax7.yaxis.set_minor_locator(AutoMinorLocator(5))
grid(ax7)
ax7.legend(frameon=False, fontsize='x-small')
ax7.text(500,8, 'Earthquake magnitudes above the line should be detectible.')
ax7.text(500,7.6, 'Earthquake magnitudes close to the line will have poor signal to noise ratio.')
ax7.text(8500,1, 'Earthquake magnitudes below the line are not detectible.')
ax7.text(8100,0.6, eq)
fig.text(0.05, 0.95, 'Earthquake magnitude estimation formulae based on:')
fig.text(0.05, 0.935, 'Lower bandpass filter frequency of 0.7 Hz.')
fig.text(0.05, 0.92, 'Upper bandpass filter frequency should not significantly clip signal.')
fig.text(0.05, 0.905, 'Max amplitude/1e-6 and distance in km used in formulae.')
fig.text(0.95, 0.935, 'Background noise sample size = '+str(bnsamp)+' s.', ha = 'right')
fig.text(0.95, 0.92, 'Test Period Start: '+bnstart.strftime(' %d/%m/%Y %H:%M:%S UTC'), ha = 'right')
fig.text(0.95, 0.905, 'Test Period End: '+(bnstart+bnsamp).strftime(' %d/%m/%Y %H:%M:%S UTC'), ha = 'right')
#adjust subplots for readability
plt.subplots_adjust(hspace=0.3, wspace=0.1, left=0.05, right=0.95, bottom=0.05, top=0.89)
#print filename on bottom left corner of diagram
# Set Directory for output Plots
pics = "D:/Pictures/Raspberry Shake and Boom/2024/" # Edit to suit **** Enter data****
filename = pics+stn+oput+str(filt[2])+'Hz'+bnstart.strftime('%Y%m%d %H%M%S UTC'+'.png')
fig.text(0.05, 0.02,filename, size='x-small')
# add github repository address for code
fig.text(0.95, 0.02,'https://github.com/sheeny72/RPiSandB', size='x-small', ha='right')
plt.savefig(filename)
# show the final figure
plt.show()